Coursera 吴恩达 (Andrew Ng) “Machine Learning” 课程笔记
机器学习是什么
监督学习
无监督学习
单变量线性回归(Linear Regression with One Variable)
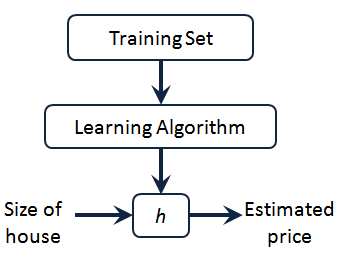
模型表示
我们将要用来描述这个回归问题的标记如下:
$m$ 代表训练集中实例的数量 我将在整个课程中用小写的$m$来表示训练样本的数目
$x$ 代表特征/输入变量
$y$ 代表目标变量/输出变量
$\left( x,y \right)$ 代表训练集中的实例
$({x}^{(i)},{y}^{(i)})$ 代表第$i$ 个观察实例
$h$ 代表学习算法的解决方案或函数也称为假设(hypothesis)
代价函数
我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价函数 $J \left( \theta_0, \theta_1 \right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( h_{\theta}(x^{(i)})-y^{(i)} \right)^{2}$最小。
我们绘制一个等高线图,三个坐标分别为$\theta_{0}$和$\theta_{1}$ 和$J(\theta_{0}, \theta_{1})$:
梯度下降的直观理解
梯度下降算法如下:
${\theta_{j}}:={\theta_{j}}-\alpha \frac{\partial}{\partial {\theta_{j}}}J\left(\theta \right)$
描述:对$\theta $赋值,使得$J\left( \theta \right)$按梯度下降最快方向进行,一直迭代下去,最终得到局部最小值。其中$a$是学习率(learning rate),它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。
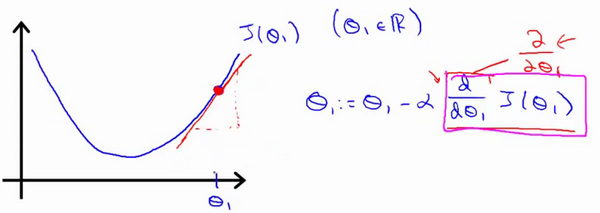
这就是我梯度下降法的更新规则:${\theta_{j}}:={\theta_{j}}-\alpha \frac{\partial}{\partial {\theta_{j}}}J\left( \theta \right)$
让我们来看看如果$a$太小或$a$太大会出现什么情况:
如果$a$太小了,即我的学习速率太小,可能会很慢,因为它会一点点挪动,它会需要很多步才能到达全局最低点。
如果$a$太大,那么梯度下降法可能会越过最低点,甚至可能无法收敛,下一次迭代又移动了一大步,越过一次,又越过一次,一次次越过最低点,直到你发现实际上离最低点越来越远,所以,如果$a$太大,它会导致无法收敛,甚至发散。
梯度下降的线性回归
我们将用到此算法,并将其应用于具体的拟合直线的线性回归算法里。
梯度下降算法和线性回归算法比较如图:

对我们之前的线性回归问题运用梯度下降法,关键在于求出代价函数的导数,即:
$j=0$ 时:
$j=1$ 时:
则算法改写成:
Repeat {
${\theta_{0}}:={\theta_{0}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{\left({{h}_{\theta}}({{x}^{(i)}})-{{y}^{(i)}} \right)}$
${\theta_{1}}:={\theta_{1}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{\left(\left({{h}_{\theta}}({{x}^{(i)}})-{{y}^{(i)}} \right)\cdot {{x}^{(i)}} \right)}$
}
我们刚刚使用的算法,有时也称为批量梯度下降。实际上,在机器学习中,通常不太会给算法起名字,但这个名字”批量梯度下降”,指的是在梯度下降的每一步中,我们都用到了所有的训练样本,在梯度下降中,在计算微分求导项时,我们需要进行求和运算,所以,在每一个单独的梯度下降中,我们最终都要计算这样一个东西,这个项需要对所有$m$个训练样本求和。因此,批量梯度下降法这个名字说明了我们需要考虑所有这一”批”训练样本,而事实上,有时也有其他类型的梯度下降法,不是这种”批量”型的,不考虑整个的训练集,而是每次只关注训练集中的一些小的子集。在后面的课程中,我们也将介绍这些方法。
如果你之前学过线性代数,有些同学之前可能已经学过高等线性代数,你应该知道有一种计算代价函数$J$最小值的数值解法,不需要梯度下降这种迭代算法。在后面的课程中,我们也会谈到这个方法,它可以在不需要多步梯度下降的情况下,也能解出代价函数$J$的最小值,这是另一种称为正规方程(normal equations)的方法。实际上在数据量较大的情况下,梯度下降法比正规方程要更适用一些。
多变量线性回归(Linear Regression with Multiple Variables)
多维特征
增添更多特征后,我们引入一系列新的注释:
$n$ 代表特征的数量
${x^{\left( i \right)}}$代表第 $i$ 个训练实例,是特征矩阵中的第$i$行,是一个向量(vector)。
${x}_{j}^{\left( i \right)}$代表特征矩阵中第 $i$ 行的第 $j$ 个特征,也就是第 $i$ 个训练实例的第 $j$ 个特征。
支持多变量的假设 $h$ 表示为:$h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+…+{\theta_{n}}{x_{n}}$,
这个公式中有$n+1$个参数和$n$个变量,为了使得公式能够简化一些,引入$x_{0}=1$,则公式转化为:$h_{\theta} \left( x \right)={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+…+{\theta_{n}}{x_{n}}$
此时模型中的参数是一个$n+1$维的向量,任何一个训练实例也都是$n+1$维的向量,特征矩阵$X$的维度是 $m*(n+1)$。 因此公式可以简化为:$h_{\theta} \left( x \right)={\theta^{T}}X$,其中上标$T$代表矩阵转置。
多变量梯度下降
与单变量线性回归类似,在多变量线性回归中,我们也构建一个代价函数,则这个代价函数是所有建模误差的平方和,即:$J\left( {\theta_{0}},{\theta_{1}}…{\theta_{n}} \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( h_{\theta} \left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}}$ ,
其中:$h_{\theta}\left( x \right)=\theta^{T}X={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+…+{\theta_{n}}{x_{n}}$ ,
当$n>=1$时,
计算代价函数: $J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {h_{\theta}}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}}$ 其中:${h_{\theta}}\left( x \right)={\theta^{T}}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+…+{\theta_{n}}{x_{n}}$
梯度下降法实践1-特征缩放
在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
最简单的方法是令: ,其中 ${\mu_{n}}$ 是平均值,${s_{n}}$ 是标准差。
梯度下降法实践2-学习率
梯度下降算法的每次迭代受到学习率的影响,如果学习率$a$过小,则达到收敛所需的迭代次数会非常高;如果学习率$a$过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
通常可以考虑尝试些学习率:
$\alpha=0.01,0.03,0.1,0.3,1,3,10$
正规方程
正规方程是通过求解下面的方程来找出使得代价函数最小的参数的:$\frac{\partial}{\partial{\theta_{j}}}J\left( {\theta_{j}} \right)=0$ 。 假设我们的训练集特征矩阵为 $X$(包含了 ${{x}_{0}}=1$)并且我们的训练集结果为向量 $y$,则利用正规方程解出向量 $\theta ={{\left( {X^T}X \right)}^{-1}}{X^{T}}y$ 。 上标T代表矩阵转置,上标-1 代表矩阵的逆。设矩阵$A={X^{T}}X$,则:${{\left( {X^T}X \right)}^{-1}}={A^{-1}}$
梯度下降与正规方程的比较:
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率$\alpha$ | 不需要 |
| 需要多次迭代 | 一次运算得出 |
| 当特征数量$n$大时也能较好适用 | 需要计算${{\left( {{X}^{T}}X \right)}^{-1}}$ 如果特征数量n较大则运算代价大,因为矩阵逆的计算时间复杂度为$O\left( {{n}^{3}} \right)$,通常来说当$n$小于10000 时还是可以接受的 |
| 适用于各种类型的模型 | 只适用于线性模型,不适合逻辑回归模型等其他模型 |
附加内容(可选)
$\theta ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y$ 的推导过程:
$J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {h_{\theta}}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}}$ 其中:${h_{\theta}}\left( x \right)={\theta^{T}}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+…+{\theta_{n}}{x_{n}}$
将向量表达形式转为矩阵表达形式,则有$J(\theta )=\frac{1}{2}{{\left( X\theta -y\right)}^{2}}$ ,其中$X$为$m$行$n$列的矩阵($m$为样本个数,$n$为特征个数),$\theta$为$n$行1列的矩阵,$y$为$m$行1列的矩阵,对$J(\theta )$进行如下变换
$J(\theta )=\frac{1}{2}{{\left( X\theta -y\right)}^{T}}\left( X\theta -y \right)$
$=\frac{1}{2}\left( {{\theta}^{T}}{{X}^{T}}-{{y}^{T}} \right)\left(X\theta -y \right)$
$=\frac{1}{2}\left( {{\theta}^{T}}{{X}^{T}}X\theta -{{\theta}^{T}}{{X}^{T}}y-{{y}^{T}}X\theta -{{y}^{T}}y \right)$
接下来对$J(\theta )$偏导,需要用到以下几个矩阵的求导法则:
$\frac{dAB}{dB}={{A}^{T}}$
$\frac{d{{X}^{T}}AX}{dX}=2AX$
所以有:
$\frac{\partial J\left( \theta \right)}{\partial \theta}=\frac{1}{2}\left(2{{X}^{T}}X\theta -{{X}^{T}}y -{}({{y}^{T}}X )^{T}-0 \right)$
$=\frac{1}{2}\left(2{{X}^{T}}X\theta -{{X}^{T}}y -{{X}^{T}}y -0 \right)$
$={{X}^{T}}X\theta -{{X}^{T}}y$
令$\frac{\partial J\left( \theta \right)}{\partial \theta}=0$,
则有$\theta ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y$